4075. Рекурсивная последовательность

Последовательность a_i целых чисел задана следующим образом:

a_i = b_i (для i ≤ k),

a_i = c₁ a_i-1 + c₂ a_i-2 + ... + c_k a_i-k (для i > k),

где b_j и c_j (1 ≤ j ≤ k) – заданные целые числа. Для заданного n следует вычислить a_n и вывести его по модулю 10⁹.

Вход. Первая строка содержит количество тестов t. Каждый тест состоит из четырех строк:

k – количество элементов (c) и (b) (1 ≤ k ≤ 10);

b₁, ..., b_k (0 ≤ b_j ≤ 10⁹) – k целых чисел, разделенных пробелом;

c₁, ..., c_k (0 ≤ c_j ≤ 10⁹) – k целых чисел, разделенных пробелом;

n – натуральное число (1 ≤ n ≤ 10⁹).

Выход. В точности t строк, каждая из которых содержит значение a_n по модулю 10⁹ для каждого теста.

Пример входа	Пример выхода
3 3 5 8 2 32 54 6 2 3 1 2 3 4 5 6 6 3 24 354 6 56 57 465 98765432	8 714 257599514

РЕШЕНИЕ

математика – возведение матрицы в степень

Анализ алгоритма

При n ≥ k воспользуемся соотношением:

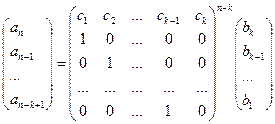
Возведение матрицы в степень реализуем за время O(log₂(n – k)).

Если n < k, то ответ выведем из соответствующей ячейки массива b.

Реализация алгоритма

Объявим модуль MOD, по которому будут производиться все вычисления. Переопределим типы vi (вектор) и vvi (матрица).

#define MOD 1000000000

typedef vector<long long> vi;

typedef vector<vector<long long> > vvi;

Умножение матрицы a на матрицу b. Все вычисления производятся по модулю mod.

vvi mult(vvi a, vvi b, int mod)

{

int i, j, k, s, n = a.size();

vvi c(n, vi(n));

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

for(s = k = 0; k < n; k++) s = (s + a[i][k] * b[k][j]) % mod;

c[i][j] = s;

}

return c;

}

Умножение матрицы a на вектор b.

vi mult(vvi a, vi b, int mod)

{

int i, j, k, s, n = a.size();

vi c(n, 0);

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

c[i] = (c[i] + a[i][j] * b[j]) % mod;

return c;

}

Возведение матрицы a в степень k.

vvi pow(vvi a, int k, long long mod)

{

int i, n = a.size();

vvi res(n, vi(n, 0));

for(i = 0; i < n; i++) res[i][i] = 1;

while (k > 0)

{

if (k % 2) res = mult(res, a, mod);

a = mult(a, a, mod);

k /= 2;

}

return res;

}

Основная часть программы. Для каждого теста читаем входные данные.

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&k);

b.assign(k,0);

Изначально положим b = (b_k, b_k-1, …, b₂, b₁).

for(i = k - 1; i >= 0; i--) scanf("%lld",&b[i]);

m.assign(k, vector<long long>(k,0));

Значения c_i считываем прямо в первую строку матрицы m. Заполняем остальные строки матрицы m.

for(i = 0; i < k; i++) scanf("%lld",&m[0][i]);

for(i = 1; i < k; i++) m[i][i-1] = 1;

Если n ≥ k, то производим вычисления по указанной в анализе задачи формуле.

scanf("%d",&n);

if (n >= k)

{

m = pow(m, n - k, MOD);

b = mult(m, b, MOD);

printf("%lld\n",b[0]);

}

Если n < k, то ответ берем из соответствующей ячейки массива b.

else

printf("%lld\n",b[k-n]);

}